你在这里
对数应变的导数
星期日,2007-07-01 20:21 -Banerjee Biswajit
你们中的一些人可能处理的问题涉及到中等强度的压力。对数应变或亨基应变是解决这类问题的一种有用的应变测量方法。特别是,如果您处理大应变模拟的数值,您将经常需要计算对数应变的材料时间导数。
在80年代中期,安猪,唐纳德·卡尔森,莫顿Gurtin他们的同事写了一系列的论文,涉及诸如应变测量,如何求导,以及如何求解包含张量的线性方程等问题。这些工作大多来自宾夕法尼亚州匹兹堡的卡耐基梅隆大学。
这篇文章是为了提醒大家,对数应变的物质导数的公式取决于拉伸张量的独立特征值的数量。它还可以作为查找其中一些公式的快速参考。
回想一下变形梯度张量,因为它有一个正行列式,可以被乘法分解成a对称的部分和部分正交部分,即
![]()
在拉伸方面,广义的n阶材料应变量和空间应变量为

拉伸的光谱分解可以写成
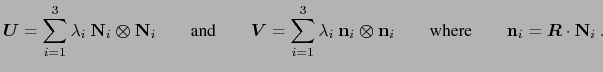
因此,我们也可以将应变测量写成

如果取n趋于0时的极限,就会得到材料和空间的对数应变(证明这个很有趣)
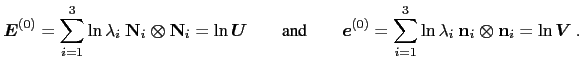
注意,在这种情况下,材料应变和空间应变具有相同的特征值。
回想一下,柯西应力和变形速率张量(更好地称为拉伸张量?)是幂共轭的。那么问题来了:什么量的幂与亨基应变的物质导数共轭,也就是说,找到这样的应力测量
![]()
结果是,当应变的主轴保持固定时
![]()
然而,这在一般情况下是不正确的,下面的公式来自[1]。具体的表达非常复杂,你可以在Hoger的论文中找到它们。
案例1:
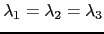
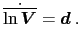
案例2:
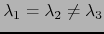
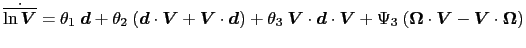
案例3:
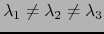

同时,
案例1:
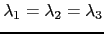
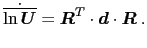
案例2:
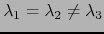
![$\displaystyle \dot{\overline{\ln\ensuremath{\boldsymbol{U}}}} = \ensuremath{\bo…<br />…ol{d}}\cdot\ensuremath{\boldsymbol{V}}\right]\cdot\ensuremath{\boldsymbol{R}}~.$](http://www.eng.utah.edu/~banerjee/iMechanica/DerivLogStrain/img17.png)
案例3:
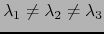
![{方程*}\ \开始开始{对齐}\点{\眉题{\ ln \ ensuremath {\ boldsymbol{你}}}}…< br /> ... 波尔{V}} ^ 2) \] \ cdot \ ensuremath {\ boldsymbol {R}} ~。结束\{对齐}结束\{方程*}](http://www.eng.utah.edu/~banerjee/iMechanica/DerivLogStrain/img19.png)
如果你知道在过去的20年里在这方面有任何进一步的简化和发展,或者如果你需要进一步澄清这些方程中使用的任何量,请评论。
»
- Biswajit Banerjee的博客
- 登录或注册发表评manbetx体育论
- 109502年读

评论
对数自旋
嗨Biswajit,
近20年来IMO的主要发展是证明了肖等人的关系
Xiao et al.[1]表明,存在一种独特的自旋——他们称之为对数自旋——它确保了上述所有可能v的等价性。在一系列论文中,他们从多个方向探索了这个问题。共轭应力的问题在b[2]中得到了最好的处理(一篇相当晦涩的论文,但非常值得一读)。它们表明,通常在拉格朗日意义上考虑的共轭应力和应变的整个概念(参见:的广泛讨论奥格登的书-本主题的最佳主要来源)可以推广到欧拉应力和应变。
安迪
参考文献:
[10]肖,H.,布鲁恩斯,O. T.和迈耶斯,A.,对数应变,对数自旋和对数速率。力学学报,32(2),1997。doi = 10.1007/BF01213020
[10] Xiao, H., Bruhns, O. T.和Meyers, A.,欧拉和拉格朗日的客观共轭率和统一工作共轭关系。力学文献,
50, 1015—1045,1998。
回复:对数应变/旋转
安迪,
谢谢你给我指出肖,布鲁恩斯,迈耶斯的论文。关于他们在有限变形弹塑性方面的工作的一个很好的概述,可以在他们的评论文章“超越小变形的弹塑性”中找到,力学学报,182,31-111 (2006),DOI10.1007 / s00707 - 005 - 0282 - 7。
我注意到的一件事是,这些作者在做弹塑性变形时,从欧拉拉伸张量(变形速率张量)的加性分解开始。许多其他作者说,这样的分解是非物理的,人们应该严格使用变形梯度的乘法分解,然后推导出相应的拉伸张量的加性分解。哪种方法是正确的?
此外,人们试图避免速率形式的弹性方程(特别是Truesdell的低弹性),而倾向于超弹性或状态方程(在大多数情况下可以从势导出)等方法。你认为哪个更好,为什么?
Biswajit
固体力学中的HIll不变性
Biswajit,
这是一本必须阅读的书,以获得对这些问题的正确看法-应用力学进展。它不涉及价值合并问题,但还有很多值得关注的地方。
至于客观汇率,真正重要的是这两种汇率之间的转换,以便将任何一种汇率转换为另一种汇率。最终,决定什么样的描述是最好的是一个物理问题。例如,您可能已经注意到,当应力本构方程以速率表示时,超弹性对应于特鲁斯戴尔速率。
- - - - - -阿米特
目标利率
阿米特表示感谢。希尔的论文确实澄清了一些问题,值得仔细阅读。根据我的理解,基本的问题是是否从一开始就使用非线性弹性模型,还是使用线性胡克定律的扩展。各种客观速率的不一致是由于胡克定律应用不当造成的。我更愿意从一个超弹性模型开始,然后从中推导出速率方程(如果必要的话)。然而,没有一种独特的方法使这种速率方程成为客观的。这就是为什么许多人完全避免使用税率表的原因。
我不知道特鲁斯戴尔率会导致超弹性。由于Jaumann和Green-Naghdi速率只是特鲁斯戴尔速率的特例它们不会导致超弹性,我不明白特鲁斯戴尔速率怎么会导致超弹性。在Simo和Hughes, Computational Inelasticity,第258页中对这个问题有很好的讨论(有参考文献)。事实上,要使一个客观速率方程由势导出,必须满足一组强的伯恩斯坦相容条件。
另一方面,引用林,布鲁克斯和贝滕的话。J.可塑性,2006,22,p. 1830,在Xiao等人的研究中证明只有利用基尔霍夫(或柯西)应力的对数旋转率的准弹性方程与弹性是一致的这是一个相当有力的说法,需要进一步的研究。请注意,对数旋转率的物理意义与所有其他弹性的客观速率方程一样存在同样的缺陷。
truesdell率
Biswajit,
我没有找到时间来跟上机械,所以这个迟到的回应,因为我刚刚看到了你的这个笔记。万博manbetx平台特鲁斯德尔速率是基尔霍夫应力随变形梯度向后拉的时间导数,由变形梯度向前推进乘以J(或J^-1,我忘了是哪个)换句话说,它基本上是基尔霍夫应力的李氏导数到J或J^-1的倍。
如果你取柯西应力的标准超弹性本构方程,取材料时间导数,然后寻找最自然的客观速率,我相信你最终会得到特鲁斯戴尔速率。
然后
\mathbf{F}^T)
因此

如果你把左边写成柯西应力和J的形式,你会得到特鲁斯戴尔速率乘以J(我相信),所以你除以J,就完成了。rhs是本构方程。对于真戴尔率(再次乘以或除以一个合适的因子),如超弹性所建议的
对数速率和其他欧拉速率
阿米特,
谢谢你的评论。这可能会被Henry Tan的学生们的评论淹没,但我想提一下,我已经把我的有限元课程的一些笔记转换成wiki形式,放在了Wikiversity上。链接是
http://en.wikiversity.org/wiki/Nonlinear_finite_elements/Objective_stress_rates
(注:我用自己编写的LaTeX到Wiki的自动转换器来转换我的LaTeX文件。转换器里可能还有bug。如果你发现任何看起来不合理的地方,请纠正它。)
关于欧拉应变速率,Andy Norris的下面这篇文章是一个很好的参考资料,它把很多东西放在了上下文中。
欧拉共轭应力和应变,
arXiv: 0708.2736
Biswajit
来自超弹性的客观比率
Biswajit,
那么你是否同意各向同性超弹性所暗示的自然客观速率是基尔霍夫应力的真实速率?
- - - - - -阿米特
阿米特,和你一样
阿米特,
正如你之前提到的,特鲁斯德尔速率是基尔霍夫应力的李氏导数(向前推/向后拉操作以总运动的雅可比矩阵进行)。所以你的问题可以重新表述为:这个特定的李氏导数会导致一个“自然的”客观空间比率吗?我不确定。
多年来,John Dienes(例如:在这里和这里),主张只利用推/拉运动的旋转部分的李氏导数(即相当于格林-纳吉迪速率的旋转速率)。美国国家实验室使用的许多密码都采用了Dienes的方法。在我天真的头脑中,这种方法似乎更自然,因为我有一种感觉,我可以想象正在发生的事情,这似乎是直觉。然而,在运动的李氏导数中,仅仅使用旋转似乎在数学上是不自然的。
关于各向同性超弹性,我觉得我们可以选择任何我们觉得方便的速率。问题不在于速率本身,而在于我们如何为空间速率方程找到合适的材料常数。如果我们从圣维南-基尔霍夫材料开始,那么空间速率方程取决于变形梯度。或者我们可以从空间构型的总本构方程出发,得到依赖于变形梯度的材料速率方程。
我认为最简单的方法是做实验,在材料或空间构型中找到一个总本构方程,然后使用在空间/材料构型中需要的任何速率和度量来实现功共轭。
Biswajit
对任何价格都没有偏好
Biswajit,
就内容而言,我同意你所说的大部分内容,除了我的问题的措辞:不,我没有解决任何“自然”客观比率的问题。没有,因为速率之间的转换是重要的(正如我在之前的一篇关于力学的文章中所说的),它们之间的关系在速度梯度中是线性的,等等。万博manbetx平台
所以我对自然客观利率的问题绝对不感兴趣——我认为这不是一个问题。但我确实认为,各向同性超弹性首先最自然地导致了特鲁斯戴尔速率(这可能也是特鲁斯戴尔提出这个观点的原因)。
在全本构方程的问题上,我与你意见不同。对于一个初始应力来源未知的物体,确定其总本构方程是绝对不可能的。这种物体的低弹性仍然可以测量——这是Biot在任意受力状态下增量变形的基础工作背后的主要原因之一。
- - - - - -阿米特
Truesdell率与1级低弹性材料
阿米特,
我对你用的“自然”这个词感到困惑。我重新阅读了你之前的一篇评论,在那篇评论中,你展示了特鲁斯戴尔速率可以从超弹性本构关系中一致地推导出来。我同意特鲁斯戴尔利率似乎是自然的。
我不知道Biot研究增量变形背后的原因。事实上,除了那些关于孔隙弹性的论文外,我没有读过Biot的任何论文(尽管我知道Biot在材料稳定性的文献中被引用了很多)。你能给我指出一些Biot的相关论文吗?或者你说的是1965年出版的《增量变形力学》吗?
我更关心的是具有两个弹性参数的各向同性材料,这些参数与变形梯度无关(或柯西应力-对于低弹性材料)。如果你看一下文献,大多数弹性速率方程使用的是0级的低弹性模型,这显然不是弹性的,也就是说,该模型不能从存储的能量势中推导出来。
显然,如果我们需要一个速率方程来描述我们的材料,并期望我们的材料是弹性的,一个简单的方法是使用1级的低弹性模型(例如,参见Truesdell和Noll的非线性力学场论中的公式99.19,404页)。我只是不知道如何设计一个实验,用已知的实验应力-应变数据来确定该模型所需的五个无维材料常数。
Biswajit
大弹性应变
我有兴趣地阅读了你的评论,并且对大弹性应变的问题相当陌生,欢迎澄清在大(即拉伸比超过1.4)与速率无关的弹性应变的背景下,对数应变的适当共轭应力是什么。
模拟应变仪
沪元
我试图得到我的模型的应变,并将其与应变计得到的实验结果进行比较。
所以,我不知道从输出历史中得到哪种应变。
谢谢。
对数压力/旋转
Biswajit,
我真的没有资格给出明确的答案,因为我在这两个主题上都没有想过或做过很多事情。我的总体感觉是,如果乘法分解和加性分解都有支持者,那么每一个都有一定的优势。每一种不同的分解都是另一种运动学描述,应该受到欢迎!这让我想起了去年的一篇很好的论文:
何庆春,郑庆生,大不可压缩变形的分解,力学学报,2006。DOI 10.1007 / s10659 - 006 - 9080 - 2
作者表明,每一个不可压缩变形都可以分解为三个垂直的单剪切,在旋转之前或之后。这是一个分解的例子,为变形的运动学提供了新的见解。另一个很好的例子是布朗热和海斯的一个美丽的结果,它扩展了极性分解的整个概念:
刘建军,刘建军,张建军,张建军,非剪切三联和扩展的极分解变形梯度,国际非线性力学学报,36,399- 420,2001。
他们表明,极性分解只是一种基于材料方向三元组的更一般的分解类型的特殊情况:非剪切三元组。
至于低弹性,在我有限的经验中,它可能来自微观结构模型,例如颗粒组合(土壤模型),所以在这些情况下使用它似乎很自然。这显然不适合大多数情况。
也许在这些事情上有第一手经验的人可以评论一下。
安迪
回复:对数应变/旋转
安迪,
谢谢你的推荐信。我在博客上发表了一篇关于低弹性及其问题的文章http://万博manbetx平台m.limpotrade.com/node/1652。它不是全面的,但应该给我们的读者一个关于利害攸关的问题的想法。
有趣的解决方案
我喜欢做那些令人困惑的问题,知道有一种方法是很神奇的
计算发展的复杂性和混乱程度。我要试试这个
计算方法,计算我最喜欢的复杂问题。