用户登录

我们讨论的内容

你在这里

首页»博客»Biswajit Banerjee的博客

另一个“直截了当”的计算

星期四，2007-09-13 21:10 -Banerjee Biswajit
教育
次弹性

按照安迪的建议，我一直在读埃利斯·迪尔的书连续介质力学［1]．在书的第75页，我们找到了
众所周知，各向同性低弹性的本构方程
物质可以从储存的能量函数中得到，只有当

$\displaystyle \lambda + \mu = 0<br /> $

在哪里\λ美元和\μ美元是Lame常数。

这个结果的推导可以追溯到Simo和Pister在1984年的一篇重要论文中提到的“一个简单的计算”[2]．
不幸的是，计算结果对我来说并不是特别简单。在得出这个结果时，任何帮助都将不胜感激。

让我来说明这个问题。

通常，对于各向同性低弹性材料，我们假设空间弹性张量具有以下形式

$ \ displaystyle \ mathsf {c} _ {ijkl} = \λ~ \ delta_ {ij} ~ \ delta_ {kl} + < br / > \μ~ (\ delta_{本土知识}~ \ delta_ {jl} + \ delta_ {jk} ~ \ delta_{他})< br / > $

如果$ \ boldsymbol {\ mathsf {C}} $是材料弹性张量吗

$ \ displaystyle \ mathsf {c} _ {ijkl} = f f {jJ} {2} ~ f f{你}{kK} ~ ~ ~ \ mathsf {c} _ {ijkl} < br / > $

在哪里$ \ ensuremath {\ boldsymbol {F}} $为变形梯度。

我们可以把这个关系反过来得到

$ \ displaystyle \ mathsf {C} _ {IJKL} = F ^ {1} _ {2} ~ F ^ {1} _ {Jj} ~ F ^ {1} _ {Kk} ~ F ^{1} _{你}~ < br / > \ mathsf {C} _ {IJKL} < br / > $

代入for表达式$ \ mathsf {c} _ {ijkl} $我们得到了

$\displaystyle \begin{align}<br /> \mathsf{C}_{IJKL} = &<br /> \lambda~(\ensuremath{\bolds…<br />…{\boldsymbol{F}}^{-1}\cdot\ensuremath{\boldsymbol{F}}^{-T})_{JK}]<br /> \end{aligned}$

如果我们定义

$\displaystyle \ensuremath{\boldsymbol{C}}= \ensuremath{\boldsymbol{F}}^T\cdot\ensuremath{\boldsymbol{F}}<br /> $

我们得到了

$ \ displaystyle \ mathsf {C} _ {IJKL} = < br / > \λ~ C ^ {1} _ {IJ} ~ C ^ {1} _ {KL} + < br / > \μ(C ^{1} _{翼}~ C ^ {1} _ {JL} + C ^{1} _{他}~ C ^ {1} _ {JK}] < br / > $

现在，如果物质定律可以从储存能量的函数推导出来，我们必须

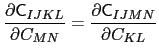
$\displaystyle \ensuremath{\frac{\partial \mathsf{C}_{IJKL}}{\partial C_{MN}} = \ensuremath{\frac{\partial \mathsf{C}_{IJMN}}{\partial C_{KL}} <br /> $

Simo写道，如果我们代入表达式for$ \ mathsf {C} _ {IJKL} $并利用上述条件，直接计算得出

美元\ displaystyle(\λ+ \μ)~ C ^ {1} _ {KL} (C_ {IM} ^ {1} ~ C_{约}^ {1}+ C_{在}^ {1}~ C…<br />…=(\λ+ \μ)~ C ^ {1} _ {MN} (C_{本土知识}^ {1}~ C_ {JL} ^ {1} + C_{他}^ {1}~ C_ {JK} ^{1})美元

（1）

这就给出了我们需要的条件

$\displaystyle \lambda + \mu = 0<br /> $

我的问题是关于推导方程(1）.

我接着回顾了这一点

$\displaystyle \ensuremath{\frac{\partial \ensuremath{\boldsymbol{C}}^{-1}}{\par…<br />…{C}} ^ {1} \ cdot \ ensuremath {\ boldsymbol {T}} \ cdot \ ensuremath {\ boldsymbol {C}} ^ {1} < br / > $

在索引符号中

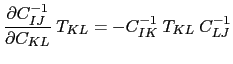
美元\ displaystyle \ ensuremath{\压裂{\部分C ^ {1} _ {IJ}}{\部分C_ {KL}}} ~ T_ {KL} =识别- C ^{1} _{本土知识}~ T_ {KL}识别~ C ^ {1} _ {LJ} < br / > $

这就给出了公式(利用的对称性$ \ ensuremath {\ boldsymbol {C}} $）

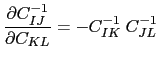
美元\ displaystyle \ ensuremath{\压裂{\部分C ^ {1} _ {IJ}}{\部分C_ {KL}}} = - C ^{1} _{本土知识}~ C ^ {1} _ {JL} < br / > $

求导后得到

$\displaystyle \begin{align}<br /> \ensuremath{\frac{\partial \mathsf{C}_{IJKL}}{\pa…<br />…} ~ C ^ {1} _ {LN} ~ C ^ {1} _ {JK} + < br / > C ^{1} _{他}~ C ^ {1} _ {JM} ~ C ^ {1} _ {KN}] < br / > \{对齐}$

和

$\displaystyle \begin{align}<br /> \ensuremath{\frac{\partial \mathsf{C}_{IJMN}}{\pa…<br />…} ~ C ^ {1} _ {LN} ~ C ^ {1} _ {JM} + < br / > C ^{1} _{在}~ C ^ {1} _ {JK} ~ C ^ {1} _ {LM}] < br / > \{对齐}$

等于这两个，我们看到消掉的项是

美元\ displaystyle \λ~ C ^ {1} _ {IJ} ~ C ^{1} _{公里}~ C ^ {1} _ {LN} ~, ~ ~ < br / > \μC ~ ^ {1} _ {IM} ~ C ^ {1} _ {JK} ~ C ^ {1} _ {LN} ~, ~ ~ < br / > \μC ~ ^{1} _{翼}~ C ^ {1} _ {JM} ~ C ^ {1} _ {LN} < br / > $

这就留给我们

$ \ displaystyle \开始{对齐}< br / > \λ~ C ^ {1} _ {IM} ~ C ^{1} _{约}~ C ^ {1} _ {KL} < br / > + \ m…<br />…} ~ C ^ {1} _ {LM} ~ C ^{1} _{约}+ < br / > C ^{1} _{在}~ C ^ {1} _ {JK} ~ C ^ {1} _ {LM}] < br / > \{对齐}$

我还不能从这一点推导出所需的关系

美元\ displaystyle(\λ+ \μ)~ C ^ {1} _ {KL} (C_ {IM} ^ {1} ~ C_{约}^ {1}+ C_{在}^ {1}~ C…<br />…< br / >(\λ+ \μ)~ C ^ {1} _ {MN} (C_{本土知识}^ {1}~ C_ {JL} ^ {1} + C_{他}^ {1}~ C_ {JK} ^ {1}) < br / > $

我错过了什么?


参考书目

1
e·h·迪尔。

连续介质力学:弹性、塑性、粘弹性。

CRC出版社，博卡拉顿，2007。

2
j·c·西莫和k·s·皮斯特。

有限变形速率本构方程的注释
问题:计算意义。

广告样稿,冰毒。达成。动力机械。Eng。[j] .中文杂志，1984。
»

评论

提交的Banerjee Biswajit星期五，2007-09-14 14:18。

我意识到在我自己的帖子上发表第一条评论是很不礼貌的。然而，在我忘记之前，我想写下一些关于迪尔的书的事情。

迪尔的书是我最近看到的关于连续介质力学的书中最好的一本。它为有限变形问题提供了大量有趣和有用的结果，这些结果在其他地方很难找到。这本书很可能适合作为课本使用，但我还不能肯定。

2)如果你对材料模型感兴趣，这本书是非常好的。提出了若干模型。然而，我发现关于各向异性有限弹性和有限塑性的章节太简短了，没有太多的用处。你必须阅读有关各向异性有限弹性的原始文献，Simo和Hughes的书仍然是关于有限塑性的最佳著作。

3)这本书和其他大多数关于连续介质力学的书最大的缺点是完全缺乏实验背景。我们有很多漂亮的模型。我和很多同学都想知道如何通过实验来确定模型参数。对于大变形问题，可以是非平凡的。可取之处是，在文学作品中可以找到一些零碎的想法。是时候将所有这些信息收集起来，并以易于理解的形式放入连续介质力学书中了。

Biswajit

»

提交的adminSEAS星期六，2007-09-15 08:10。

非常感谢你的帮助。我不知道这本新书。看了你的推荐信后，我要求我们图书馆订购一本。

你关于将复杂材料行为模型与实验数据联系起来的评论是正确的。这听起来像是一个非常适合jClub的主题。你对引领这样一个主题有什么想法吗?

»

提交的Banerjee Biswajit星期六，2007-09-15 17:44。

亲爱的管理员,

我不能说我在实验数据方面有专业知识，除了在金属的高应变率塑性的一个非常狭窄的范围内。然而，就可塑性而言，我相信Rebecca Brannon对事物有更广泛的看法。我会问丽贝卡·布兰农她是否有可能领导这样一个JClub主题。

这样的主题可能需要与具有有限变形弹性和粘弹性实验专业知识的人一起组织。

Biswajit

»
Temesgen Markos的照片

提交的Temesgen马科斯星期六，2007-09-15 21:52。

我想生物力学学界正在进行大量关于非线性弹性和非弹性本构关系的实验工作和参数估计。我记得大约一年前读过加州大学圣地亚哥分校生物工程系Y.C. Fung和同事的一些论文。

实验人员如何设置实验来确定某些材料是否属于某一类(各向同性与各向异性，弹性与非弹性等)，这真的很有趣。

来自这个论坛的Michelle Oyen怎么样?我想她可能对这个问题很熟悉，或者与相关社区有联系。

欢呼,

Temesgen

»

提交的Banerjee Biswajit星期二，2007-09-18 16:16。

Simo式(3.10)和Dill式(2.7.17)要求

LHS = RHS

lh = Cinv (k, l) * (Cinv(我)* Cinv (j n) + Cinv(我,n) * Cinv (j, m));
rhs = Cinv (m, n) * (Cinv (i (k) * Cinv (j l) + Cinv (l)我* Cinv (j, k));

然而，一个简单的Matlab计算表明lhs != rhs。所以我认为西莫方程是错误的因此条件+ = 0是不准确的。

下面是Matlab代码:

函数testHypo

F = [[1.1 0.2 0.3];[0.2 1.5 0.4];[0.3 0.5 0.9]];
C = f '* f;
Cinv = inv(C);

LHS = 0.0;
RHS = 0.0;
因为我= 1:3
j = 1:3
k = 1:3
l = 1:3
m = 1:3
为n = 1:3
lh = Cinv (k, l) * (Cinv(我)* Cinv (j n) + Cinv(我,n) * Cinv (j, m));
rhs = Cinv (m, n) * (Cinv (i (k) * Cinv (j l) + Cinv (l)我* Cinv (j, k));
Diff = LHS - rhs;
If (diff ~= 0)
[i j k l m n LHS RHS diff]
结束
结束
结束
结束
结束
结束
结束

随便选一个案子

I =3 j= 3 k =3 l =3 m = 2 n = 2

LHS = 2.7484

RHS = 7.3075

Diff = -4.5591

显然不是零。我认为西莫的结果是错误的。我很乐意看看是否有人能证明这一点。

Biswajit

更新:仔细想想，Simo所需要的只是diff != 0(一般情况下，尽管有些情况下它将为零)，这意味着lambda+mu = 0。所以我的测试不能证明什么。我还是想看看西莫的结果如何被证明或测试。如果我对方程做同样的测试，我也不会得到lhs = rhs，所以要么是我的方程错了，要么是西莫的方程错了。

»
安德鲁·诺里斯的照片

提交的安德鲁·诺里斯星期二，2007-09-18 18:41。

嗨Biswajit,

看看迪尔的书，他在K_{ijkl} in(2.7.16)的表达式中有一个因子J。你把J算进去了吗?

顺便说一句，我没有西蒙-皮斯特的论文，但我很想读一下。如果你有pdf文件可以发给我吗?

谢谢,

安迪

»

提交的Banerjee Biswajit星期二，2007-09-18 18:58。

J因子来源于蓄能函数和应力-应变关系的定义。这不是计算的必要部分。如果你缩并Simo方程和C_MN C_IK C_JL那么你就会得到6(+)= 12(+)如果我没算错的话。如果我的计算错了，要么是链式法则错了，要么是逆函数的导数错了。我一时看不出问题所在——也许我看得太久了，需要换个角度看问题。

Biswajit

»

提交的Banerjee Biswajit星期二，2007-09-20 19:20。

诺里斯教授指出了我的错误。问题是

1) a的逆函数的导数对称的二阶张量相对于二阶张量得到a对称的四阶张量。我的逆表达式是不对称的(也就是说，我需要再加一项，然后除以2)。

2) Andy所说的J在推导中是至关重要的。否则就得到= 0。我从Simo和Hughes的表达式开始，Computational Inelasticity, p. 256, eq. 7.1.82，其中没有因子J。你必须小心处理这些方程。我会确保从现在开始我总是使用标准方程:)

如果这些误差在上面的推导中是固定的，那么代数确实是直截了当的。

Biswajit

»
安德鲁·诺里斯的照片

提交的安德鲁·诺里斯星期五，2007-09-21 11:28。

嗨Biswajit,

这让我想起了我一直记得的一位同事的评论——我转述说:西莫的论文并不总是容易理解，但它们总是正确的。

我不知道第一部分，但第二句似乎是真的!

安迪

»

提交的Banerjee Biswajit星期二，2007-09-27 16:25。

嗨,安迪,

在过去的五年里，我几乎浏览了西莫写的每一篇论文。他早期的论文相对容易理解(如果你接受他的结果是正确的)。

Simo在塑性方面的第一个出发点是确定与优化理论中的Kuhn-Tucker条件相同的加载/卸载条件。他还带来了很多凸分析的结果，没有任何简单的解释。这使得他的语言很难理解，除非你了解基本的凸分析和优化理论。

我发现他的一些关于几何上精确的壳的论文很难读，因为我不理解他关于微分几何中一型和二型的语言。我认真阅读了大卫·福克斯(David Fox)的博士论文，才理解了其中的很多东西。我发现Theodore Frankel所著的《the Geometry of Physics》一书对于基本概念非常有用。

同样，为了理解Simo论文中的数值分析，你必须了解一点泛函分析。

一旦你掌握了这些要求，你就可以理解试卷了——但即使这样，它们也不是直截了当的。

附注:对于那些想知道这篇博文是关于什么的人，我已经把细节放在了Wikiversity上。你可以在

http://en.wikiversity.org/wiki/Nonlinear_finite_elements/Rate_form_of_hyperelastic_laws

Biswajit

»

提交的梁雪星期五，2007-09-21 22:12。

唯一的遗憾是西莫过早地离开了我们。

»
订阅评论以获得“另一个直截了当的”。计算”

最近的评论

更多的评论

辛迪加

认购辛迪加