你在这里
外延收敛(最大基底)，裂纹扩展
在本文中，我们使用变分分析技术(特别是epi-收敛理论)证明了最大熵基函数的连续性。一般来说，对于非光滑泛函，移动目标和/或约束，牛顿-莱布尼茨微积分的工具(梯度，点收敛)证明是不够的;需要集值映射、集收敛等概念。外延收敛与伽玛收敛或莫斯科收敛(广泛用于马氏体相变的数学处理)密切相关。关于凸分析和外收敛的介绍性材料必须在修订版中省略;因此，材料绝不是自成一体的。下面是一些有用的建议。我们的主要参考点是RTR和RJBW的变分分析;普林斯顿经典RTR的凸分析提供凸分析中的重要工具。对于凸优化，文本基于SB和LV的凸优化(可在线获取)是优秀的。的演讲的幻灯片为凸分析中的一些重要概念提供一个非常好的(温和的)介绍。的碑文景观。非常丰富，许多应用会引起机械师的共鸣。万博体育平台
在另一个主题(非平面裂纹扩展)上，我们将x-fem一种新的快速行进算法。这里有几个关于斜面裂缝在张力下生长的动画(非结构化四面体网格，只有超过12K个节点):较大的“时间”增量和更小的“时间”增量．这是与Chopp, Bechet和Moes (nsf - ise项目)的联合工作。我将更新这个页面，当更多的相关链接可用。
| 附件 | 大小 |
|---|---|
 maxentepi.pdf |
558.46 KB |
»
- N. Sukumar的博客
- 登录或注册发表评manbetx体育论
- 19889年读
评论
Re:最大熵基函数
Sukumar,
我试着读了你的论文，但有几个地方不太明白(你推荐的阅读清单真的很吓人:)
我的问题很基本:
1)另一个基函数空间的动机是什么?
2)最大熵基函数比其他基函数有什么优势?
我相信这些问题在文献中都有答案。然而，我也认为像iMechanica这样的论坛的一个好处是，我们可以从作者那里得到这些问题的答案，而不必花费大量的时间去理解关于特定万博manbetx平台主题的大量文献。因此，你能简单地(不严格地)解释一下为什么你在探索最大熵基，为什么这些基的连续性如此重要吗?
在一个稍微不同但相关的笔记上，我认为我们的读者会发现下面的讨论很有趣。这个讨论是约翰·贝兹写的，名为为什么数学很无聊?”．
Biswajit
Re: Max-ent basis
我只触及了表面，因此请放心，我有一种预感，除了变分分析(VA)一书的作者之外，大多数人(包括凸分析专家)都会同意您的观点。我的目的只是提供一些背景，因此链接。关于max-ent，了解无网格景观的人应该评论一下，因为这是一个公正的观点。我的个人观点如下。关于你的问题:(1)和(2)如果你追踪无网格方法中使用的基函数的根以及过去10多年来的发展(无论是SPH，径向基函数，移动最小二乘等)，一些需求已经出现在前列。(A)从有限元到无网格近似的平滑过渡(因为整个域的无网格近似往往变得昂贵);(B)边界上类似fem的行为很容易施加必要的边界条件。正如Arroyo和Ortiz(2006)的文章所揭示的那样，凸近似(phi_i >= 0)的使用是关键。基本边界条件由任何凸近似来处理，他们使用了一个改进的熵函数(与统计力学联系)来获得具有紧支持的基函数。当从Kullback-Leibler距离的角度来看，可以通过选择一个先验(权重函数)然后使用熵正则化来获得满足约束(线性再现条件)的基函数来推广这种结构----。如果你回头看，试图“纠正”SPH(恒定一致性到线性一致性)，就像在RKPM中所做的那样，有着同样的动机。现在，使用max-ent，这种方法得到了推广----，您可以纠正任何具有紧凑支持的先验(权重函数)，以构建线性完整的、紧凑支持的基函数，并将在边界(凸包的边缘)上进行插值。这是与其他无网格基函数相比的主要吸引力。在A&O的论文中可以找到凸近似的许多其他属性。 In这个文档，我提供了更多的细节，链接，以及上面的文章和许多其他相关的链接。在阅读这篇文章时，凸面优化的吸引力和地位将有望得到体现，从而从凸面分析中获得工具(如VA)的有用性。力学充满了变分公式(约束、凸、非凸、鞍点等)，似乎只有像德劳内插值一样，通过(约束)变分途径获得无网格基函数才合适。希望这提供了一些答案?
一个关于极大基的问题
亲爱的Sukumar教授:
我读了你的论文，并与Biswajit教授分享了类似的问题。看了你的回复，我还有两个具体问题:
1)是否任何紧支持的权函数都可以用来构造基函数?唯一的要求是它有紧凑的支撑?
2)我们都知道，无网格法的缺点之一是与有限元法相比，其基函数的构建成本较高。那么你的最大基评估效率如何呢?与有限元法或现有的无网格法相比，它是更耗时还是更高效?至少我从你的论文中了解到这种方法更加灵活和通用。
谢谢你！
Jinxiong
回复:最大的问题
金雄:关于你的问题:1）是的,任何连续可以使用具有紧凑型支撑的权重函数。至少需要权值连续才能得到C0基函数;如果使用更平滑的权重，可以得到更平滑的基函数(类似于mls)。如果使用恒定的重量(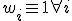
)则所有基函数在整个定义域的任意点都是非零的，因此它们不是紧支持的。几个不同权重的基函数图出现在我附上的论文中。2）没有方案可以打败有限元，如果只是直接比较基函数的计算;更现实的比较是根据所能达到的准确性和功能是否可以扩展到fem的已知极限来比较整个运行时。我还没有直接与mls进行比较(手头没有mls代码)。Marino去年在wccm上提出了一些关于这种比较的结果，我记得mls和max-ent的时间顺序是一样的。他可以回答你的问题(用精确的数字)，也可以提供更多关于他所做的计算和测试的细节。当然，最大时间将在一定程度上依赖于为满足再现(线性一致性)条件而设置的容差(如果需要12位数而不是6位数的精度，则需要额外的牛顿迭代)。我没有提到的一点是(在我看来)，在无网格方法中实现max-ent比大多数无网格基础更容易，因为人们不必担心基本边界条件的强加:如果基本边界条件要通过基本边界上的FE插值实现，则无需区分不同类型的节点和不同的区域(FE, MLS和混合/接口区域)。在机器学习中，我们必须先验地分配节点的支持大小。我在Fortran 90中有一个最大的实现，相同的代码可以用于1D, 2D和3D，可以选择选择不同的权重函数作为先验。总的来说，这提供了灵活性和易用性。
谢谢Sukumar教授!
亲爱的Sukumar,
感谢您的快速回应和详细的澄清!我完全同意你的观点，max-ent方法更灵活，与标准的无网格方法相比，具有Kronecker delta属性确实是一个独特的特征。它对处理双材料复合材料非常有用。我要试试!
Jinxiong
3 d E-FEM
Suku,
非常感兴趣的3D便士裂纹扩展-非常令人印象深刻的工作。如果你能给我发邮件或给我指出文献，我将不胜感激。
Qingda
Re: Max-ent basis
Sukumar,
谢谢你的澄清和指点。你的文章很好地介绍了无网格方法所面临的问题。既然阿罗约读了《机械》，也许他能提供进万博manbetx平台一步的见解?
Biswajit
回复:支付基础
你好,
Biswajit，我理解你的问题，为什么还有另一种无网格方法?首先，我想指出有许多无网格方法(至少有许多缩写)，但没有那么多无网格近似。移动最小二乘思想非常好，是大多数方法的基础。最大近似值提供了一种从分散的点集构造近似值的替代方法和基本原理。
我认为Suku很好地阐述了这些特殊形状功能与其他功能相比的优势。我将它们总结为:(1)在任何空间维度上高效且稳健的计算，而不仅仅是1,2或3，(2)狄利克雷bc是直接的，(3)由于它们是非负的，它们不会在冲击附近显示吉布斯型振荡，(4)对于光滑解的PDE，基于这些近似的伽勒金方法的精度非常好，因此对于给定的精度它们比FE更有效。但说实话，最让我兴奋的是它在不同领域之间建立的联系，比如凸几何、信息论、近似理论和数值方法、统计学习等。事实上，一种非常类似的方法已经被设计用于无监督统计学习，并且有人认为最大近似值在存在噪声数据的情况下具有非常强的鲁棒性，并且在高d下表现得特别好。
http://idl.ee.washington.edu/publications/thesis.pdf
最好的问候,
马里诺