用户登录

我们讨论的内容

你在这里

首页»博客»Biswajit Banerjee的博客

张量的不变量的导数

星期日，2007-05-13 21:21 -Banerjee Biswajit
教育
连续介质力学
衍生品
不变量

当你第一次开始学习有限变形塑性时，你会遇到塑性流率$ \ ensuremath {\ boldsymbol {d}} _p美元这可以从流势中得到\φ美元这样

$\displaystyle \ensuremath{\boldsymbol{d}}_p = \ensuremath{\frac{\partial \phi}{\partial \ensuremath{\boldsymbol{\sigma}}}}$

（1）

在哪里$ \ ensuremath {\ boldsymbol{\σ}}$是柯西重音。对于具有标量内变量的各向同性材料，塑料
流势可以假设为

$\displaystyle \phi \equiv \phi(p, J_2, J_3;T, q_j)美元

（2）

在哪里$ p $是压强，$ j_2, j_3 $偏应力是不变量吗$ \ ensuremath {\ boldsymbol{年代}}$，元新台币是温度，和q_j美元是内部变量。的数量$ p $，J_2美元,J_3美元定义为

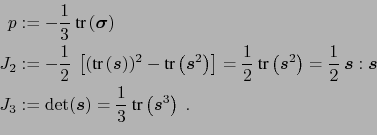
= -\ensuremath{\frac{1}{3}} \ensuremath{\ the…<br />…t{tr}\left(\ensuremath{\boldsymbol{s}}^3\right)} . \end{aligned}\end{equation*}

用链式法则可以写成

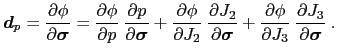
$\displaystyle \ensuremath{\boldsymbol{d}}_p = \ensuremath{\frac{\partial \phi}{…<br />…\ensuremath{\frac{\partial J_3}{\partial \ensuremath{\boldsymbol{\sigma}}}} .$

（4）

你遇到的第一个问题是如何求导数
不变量。我的第一次尝试是用组件来表达一切
然后求微分。这种方法有效，但可能很乏味。

一个有经验的机械师只会去读特鲁万博体育平台兹德尔和诺尔的书
［1然后从那本书的第26页挑出了公式。
然而，那本书用古老的德语和希伯来语符号把我吓坏了。
对于那些觉得特鲁兹戴尔和诺尔很难读懂的人来说，这是
那本书处理不变量求导问题的方式。
希望对你有用。

标量值函数的导数美元\φ(\ ensuremath {\ boldsymbol{一}})美元二阶张量的$ \ ensuremath {\ boldsymbol{一}}$可以用方向导数来定义吗

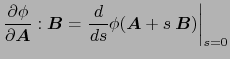
$\displaystyle \ensuremath{\frac{\partial \phi}{\partial \ensuremath{\boldsymbol…<br />…（\ensuremath{\boldsymbol{A}}+ s \ensuremath{\boldsymbol{B}}) \right\vert _{s=0}$

（5）

在哪里$ \ ensuremath {\ boldsymbol {B}} $是一个任意二阶张量。不变的I_3美元是由

$\displaystyle I_3(\ensuremath{\boldsymbol{A}}) = \det(\ensuremath{\boldsymbol{A}}) .$

（6）

因此，根据导数的定义，

\begin{equation*}\begin{aligned}\ensuremath{\frac{\partial I_3}{\partial \ensure…< br /> ...\ boldsymbol正确{B}} \) \] \ \绿色_ {s = 0}。结束\{对齐}结束\{方程*}

回想一下我们可以把张量的行列式展开成
用不变量表示的特征方程$ I_1 I_2 I_3美元使用

$\displaystyle \det(\lambda \ensuremath{\boldsymbol{\mathit{1}}}+ \ensuremath{\b…<br />…I_2 (\ ensuremath {\ boldsymbol{一}})\λ+ I_3 (\ ensuremath {\ boldsymbol{一}})。美元

（8）

利用这个展开式，我们可以写

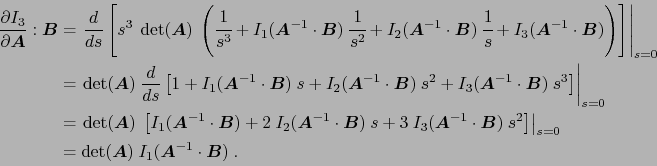
\begin{equation*}\begin{aligned}\ensuremath{\frac{\partial I_3}{\partial \ensure…< br /> ... 符号{一}}^ {1}\ cdot \ ensuremath {\ boldsymbol {B}})。结束\{对齐}结束\{方程*}

回想一下不变量I_1美元是由

$\displaystyle I_1(\ensuremath{\boldsymbol{A}}) = \ensuremath{\text{tr}\left(\ensuremath{\boldsymbol{A}}\right)} .$

（10）

因此,

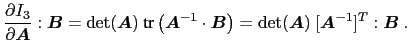
\ ensuremath {\ boldsymbol {B}}。美元

（11）

的随意性$ \ ensuremath {\ boldsymbol {B}} $然后我们有

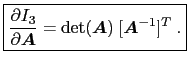
$\displaystyle \boxed{\ensuremath{\frac{\partial I_3}{\partial \ensuremath{\bol…<br />…} = \检波器(\ ensuremath {\ boldsymbol{一}})[\ ensuremath {\ boldsymbol{一}}^ {1})^ T。} $

（12）

的分量在标准正交基中$ \ ensuremath {\ boldsymbol{一}}$可以写成矩阵吗$ \ ensuremath {\ mathbf{一}}$．在这种情况下，右边对应于

矩阵的余因式。

对于另外两个不变量的导数，我们回到
特征方程

$\displaystyle \det(\lambda \ensuremath{\boldsymbol{\mathit{1}}}+ \ensuremath{\b…<br />…I_2 (\ ensuremath {\ boldsymbol{一}})\λ+ I_3 (\ ensuremath {\ boldsymbol{一}})。美元

（13）

使用与之前相同的方法，我们可以证明

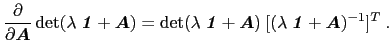
$\displaystyle \ensuremath{\frac{\partial}{\partial \ensuremath{\boldsymbol{A}}…<br />…da \ ensuremath {\ boldsymbol {\ mathit {1}}} + \ ensuremath {\ boldsymbol{一}})^ ^ T。$ {1})

（14）

左边可以展开为

\begin{equation*}\begin{aligned}\ensuremath{\frac{\partial}{\partial \ensuremat…<br />…{\partial \ensuremath{\boldsymbol{A}}}}。结束\{对齐}结束\{方程*}

因此

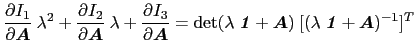
$\displaystyle \ensuremath{\frac{\partial I_1}{\partial \ensuremath{\boldsymbol{…<br />…ambda \ ensuremath {\ boldsymbol {\ mathit {1}}} + \ ensuremath {\ boldsymbol{一}})^ ^ T $ {1})

（16）

或者,

$\displaystyle (\lambda \ensuremath{\boldsymbol{\mathit{1}}}+\ensuremath{\bold…<br />…athit {1}}} + \ ensuremath {\ boldsymbol{一}})\ ensuremath {\ boldsymbol {\ mathit{1}}}。美元

（17）

展开右边，分离左边的项
给了

$\displaystyle (\lambda \ensuremath{\boldsymbol{\mathit{1}}}+\ensuremath{\bold…<br />…+ I_1 \lambda^2 + I_2 \lambda + I_3\right] \ensuremath{\boldsymbol{\mathit{1}}}$

（18）

或者,

$\displaystyle \left[\ensuremath{\frac{\partial I_1}{\partial \ensuremath{\bolds…<br />…I_1 \λ^ 2 + I_2 \λ+ I_3 \] \ ensuremath {\ boldsymbol {\ mathit{1}}}。美元

（19）

如果我们定义= 1美元和= 0美元，我们可以把上面的式子写成

$\displaystyle \left[\ensuremath{\frac{\partial I_1}{\partial \ensuremath{\bolds…<br />…I_1 \λ^ 2 + I_2 \λ+ I_3 \] \ ensuremath {\ boldsymbol {\ mathit{1}}}。美元

（20.）

集合包含各种幂的术语\λ美元，我们得到

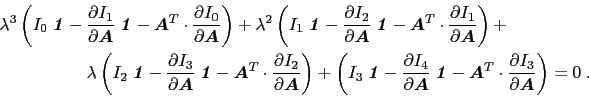
{方程*}\ \开始开始{对齐}\λ^ 3 & \离开(I_0 \ ensuremath {\ boldsymbol{\垫子…<br />…partial \ensuremath{\boldsymbol{A}}}}\right) = 0。结束\{对齐}结束\{方程*}

然后，调用任意的\λ美元，我们有

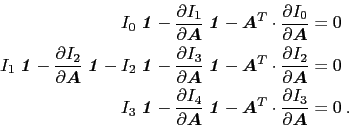
\begin{equation*}\begin{aligned}I_0 \ensuremath{\boldsymbol{\mathit{1}}}- \ensur…<br />…_3}{\部分\ ensuremath {\ boldsymbol{一}}}}& = 0。结束\{对齐}结束\{方程*}

这意味着

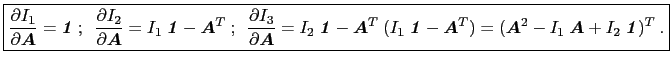
$\displaystyle \boxed{\ensuremath{\frac{\partial I_1}{\partial \ensuremath{\bol…<br />…1 \ensuremath{\boldsymbol{A}}+ I_2 \ensuremath{\boldsymbol{\mathit{1}}})^T . }$

（23）

基于上述可以推断出的其他有趣的关系是

$ \ displaystyle \ ensuremath {\ boldsymbol{一}}^ {1}= \ cfrac{1}{\侦破(\ ensuremath{\博…<br />…1 \ensuremath{\boldsymbol{A}}+ I_2 \ensuremath{\boldsymbol{\mathit{1}}}\right]$

（24）

和

$\displaystyle \ensuremath{\frac{\partial I_3}{\partial \ensuremath{\boldsymbol{A}}}} = I_3 [\ensuremath{\boldsymbol{A}}^T]^{-1} .$

（25）

回想一下,

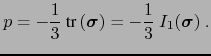
$\displaystyle p = - \ensuremath{\frac{1}{3}} \ensuremath{\text{tr}\left(\ensure…<br />…}}\right)} = -\ensuremath{\frac{1}{3}} I_1(\ensuremath{\boldsymbol{\sigma}}) .$

（26）

因此,

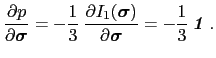
$\displaystyle \ensuremath{\frac{\partial p}{\partial \ensuremath{\boldsymbol{\s…<br />…l{\σ}}}}= - \ ensuremath{\压裂{1}{3}}\ ensuremath {\ boldsymbol {\ mathit{1}}}。美元

（27）

还记得吗

$\displaystyle J_2 = \ensuremath{\frac{1}{2}} \ensuremath{\text{tr}\left(\ensure…<br />…uremath{\boldsymbol{s}}^2\right)}\right] = -I_2(\ensuremath{\boldsymbol{s}}) .$

（28）

因此,

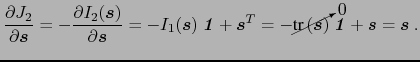
$\displaystyle \ensuremath{\frac{\partial J_2}{\partial \ensuremath{\boldsymbol{…<br />…年代ymbol{\mathit{1}}}+ \ensuremath{\boldsymbol{s}}= \ensuremath{\boldsymbol{s}} .$

（29）

最后,

$\displaystyle J_3 = \det(\ensuremath{\boldsymbol{s}}) = I_3(\ensuremath{\boldsymbol{s}}) .$

（30.）

因此,

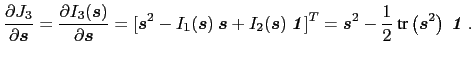
$\displaystyle \ensuremath{\frac{\partial J_3}{\partial \ensuremath{\boldsymbol{…<br />…ft(\ensuremath{\boldsymbol{s}}^2\right)} \ensuremath{\boldsymbol{\mathit{1}}} .$

（31）

把这些结果收集在一起，我们得到

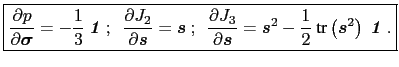
$\displaystyle \boxed{\ensuremath{\frac{\partial p}{\partial \ensuremath{\bolds…<br />…（\ensuremath{\boldsymbol{s}}^2\right)} \ensuremath{\boldsymbol{\mathit{1}}} . }$

（32）



参考书目


1
C.特鲁斯戴尔和W.诺尔。

力学的非线性场论．

斯普林格出版社，纽约，1992年。
»

评论

Amit Acharya的照片

提交的Amit Acharya星期日，2007-05-13 23:09。

Biswajit,

事实上，代数和微积分永远不会失去它的魅力。

另一种方法:通过认识到二阶张量的迹是它与单位元的内积，可以很容易地求出第一和第二不变量的导数。对于第二个不变量，将这个观察结果与链式法则结合起来。

第三个不变量，以及(可逆)张量的逆的导数更有趣。我从我的导师唐·卡尔森那里学到了以下几点。

一旦你像上面那样知道了如何对第一和第二不变量求导，然后意识到张量满足它自己的特征方程(Cayley-Hamilton定理)，然后对张量特征方程求导得到第三个不变量的导数用前两个不变量的导数表示，以及张量本身及其平方的导数。

将张量特征方程乘以张量的逆然后求导;然后，如果知道不变量的导数，那么逆函数的导数就出来了。

下一个有趣的问题是，如果这些函数的定义域是一个非平凡流形，如何做到这一切，例如，假设你的s是不可压缩的(即det s = 1)。当然，即使是逆的，也有一点问题要解决，因为所有可逆二阶张量的集合不是一个向量空间，但有一种方法可以避免，因为它至少是一个开集，并且微分的结果是，从定义域内的一点出发的足够小的偏移仍然在定义域内(这是一个要求，比如说，你对方向导数的定义是有意义的)。

最好的

阿米特

»

提交的Banerjee Biswajit星期一，2007-05-14 14:56。

阿米特,

谢谢你的指点。当我有时间的时候，我会试着把推导过程写出来，贴在这里。

你能详细解释一下为什么“所有可逆二阶张量的集合不是一个向量空间”以及它如何影响微分吗?举一个例子，当一个偏移离开歧管的情况将会很有帮助。

Biswajit

»
Amit Acharya的照片

提交的Amit Acharya星期一，2007-05-14 23:36。

Biswajit,

考虑可逆张量I和-I。它们的和是不可逆的。因此。不是向量空间。

函数在x处的微分要求函数的值定义在x + h处，h足够小。如果所涉及的函数的定义域是一个向量空间，这不是问题，即使它不是整个空间，而只是一个向量空间的开集，这也不是问题。

为了便于几何理解，考虑在三维空间中的二维壳表面上定义的标量函数φ。设h为壳层在x处的切向量，且壳层在x处不是平的。那么φ(x + h)对于每一个非零切向量h，无论多小，都不是严格定义的。出于同样的原因，方向导数的定义也变为

D /ds φ(f(s))|s=0，其中f是流形上f(0) = x的曲线。

如果(y^i)是壳层在x处的局部参数化，用梯度向量表示在x处的导数

Grad φ = φ_，i e^i其中(e^i)是参数化对应的对偶基。因此，梯度向量与壳相切，而如果φ处处都有定义，那么梯度向量将有一个垂直于壳的分量。

实际上，当在壳层的有限元实现中处理有限旋转时，当推导雅可比矩阵时，这总是会出现。

希望这对你有所帮助。

»

提交的Nachiket Gokhale星期二，2007-05-15 20:51。

你写的:

为了便于几何理解，考虑在a上定义的标量函数φ
三维空间中的二维壳面。设h为切向量
让壳层在x处不平坦，则φ(x + h)为
对于每一个非零切向量h，不管多小，都没有严格定义。

我认为这是因为点(x+h)离开了壳层表面。我说的对吗?

-Nachiket

»
Amit Acharya的照片

提交的Amit Acharya星期二，2007-05-15 21:04。

Nachiket,

是的，你说得对。

»
Amit Acharya的照片

提交的Amit Acharya星期一，2007-05-14 07:39。

当然，最简单的方法是求导。求逆函数的方法是从SS^-1 = 1开始。

»
阿提拉·科萨的照片

提交的阿提拉Kossa周六，2012-02-25 18:52。

亲爱的!

有一个棘手的问题:如果我们从定义J3=1/3*Tr[s^3]开始，为什么我们得到J3关于s的导数的不同结果?

解决方案1:

在这个博客条目的eq(32)中为:s^2 - 1/2 Tr[s^2] * 1

解决方案2:

1/3*Tr[s^3]对s求导等于s^2

[参见:Jirásek, M. and Bazant(2000):结构的非弹性分析，p. 653 eq. (D.55);或看到
Zienkiewicz & Taylor(2000):…有限元方法卷2,p. 435 eq. [A.25]

[参见:Itskov(2009):工程师的张量代数和张量分析第2版，p. 124 eq. (6.52)]

最好的问候,

阿提拉

»

提交的Banerjee Biswajit周六，2012-02-25 23:10

s是的偏差部分，Tr(s) = 0。

附注:这个评论是不相关的。请无视。

»
Amit Acharya的照片

提交的Amit Acharya周日，2012-02-26 13:41。

我承认我没有看过你提供的解决方案，也没有看过你提供的推荐信。但这里有一些你可能想要评论的想法:

1) Biswajit公式只有在求导的对称偏张量可逆时才成立。一般的无迹张量不需要满足这个条件。

2)我刚刚想到的另一个问题(我根本没有想太多)是，如果我们把J3看作是在对称偏张量空间上定义的，这是一个向量空间(据我所知)，那么计算这个空间上的可微实值函数的梯度应该会得到空间本身的一个元素——即对称偏张量。就像你说的，s²不一定是偏的，那么你认为函数J3的定义域是什么?对称偏张量，或者仅仅是对称张量，或者可逆对称偏张量?

我注意到如果我们考虑fn J3是在可逆对称偏张量的定域上定义的你和Biswajit写的公式都需要修正去掉它们的流体静力部分来得到梯度然后它们就会得到相同的公式。

»

提交的Banerjee Biswajit周日，2012-02-26 17:04。

阿米特

我已经很长时间没有考虑这些事情了，我不记得我是在哪里第一次看到这个结果的。但它确实看起来很奇怪，所以才会扭曲到它。

(2)相当深刻，我没有从这些方面考虑过。这值得论坛里的其他人更多的研究。

——Biswajit

»
阿提拉·科萨的照片

提交的阿提拉Kossa星期一，2012-02-27 02:29。

我对我的问题做了详细的推导步骤。

我认为方法二是J3导数的正确解。

但是方法1呢?

阿提拉

»

提交的Banerjee Biswajit星期一，2012-02-27 21:48。

j3

»
阿提拉·科萨的照片

提交的阿提拉Kossa星期二，2012-02-28 04:18。

亲爱的Biswajit，

当你计算d(J3)/d(sigma11)时，我想你忘了计算d(p)/d(sigma11)P本身显然取决于∑11。因此我认为这条直线上少了一项1/3。

阿提拉

»

提交的Banerjee Biswajit星期二，2012-02-28 15:14。

上面的要点是展示一种使用蛮力获得解决方案1的方法。

我们假设dJ3/dp = 0。但是，正如阿米特在其他地方指出的，dJ3/dp导数定义不清因为对于给定的p, J3可以取无限个值。

选项4,dJ3/ds = Dev[s^2]，给出了Amit指向的无痕迹解决方案，即与DevSymm流形相切的解决方案。

——Biswajit

»
Gayan Aravinda的照片

提交的Gayan Aravinda星期一，2015-10-05 08:27。

我同意阿提拉的观点。p本身是sigma11的函数而biswajit没有考虑它。我已经推导出了偏应力张量的第三个不变量对偏应力张量的直接项和间接项的导数。但这些表达式与上述表达式不同，因为p也是直接应力项的函数;上述表达式的导数应被视为乘法的导数。

Gayan

»

提交的Banerjee Biswajit星期一，2012-02-27 22:48

另一种可能性:)

J3衍生期权4

»
Amit Acharya的照片

提交的Amit Acharya星期一，2012-02-27 23:13。

这里发生的事情确实很有趣。

在不失去一般性的前提下，我们考虑(1)对对称二阶张量有效(2)对对称可逆二阶张量有效。

考虑一下你的收入。11.

第一个平等:第一个平等

第一个等式成立如果你把J_3和tr(s^3)定义为对称偏张量空间上的函数。如果你离开了tr(s) = 0的流形，那么这个关系就不成立了。

第二个等式:第二个平等

然而，第二个等式是考虑tr(.)是对称张量空间上的函数，在这个空间的导数的定义是正确的tr (s ^ 3)(1)。它可以显示被小心导数的含义和一个实值函数的梯度向量空间的梯度tr (s ^ 3)定义的歧管tr (s) = 0可以写减去从相同的函数的梯度对称二阶张量的整个空间投影在正常约束歧管。所有这些等于简单地减去s^2在I/(√3)上的投影，所以正确的结果应该是12


J3在对称开发空间中的导数——(* *)

这个结果适用于所有对称偏张量，无论是否可逆。

现在我们来看方法一:定义5和公式2和7要求J_3只能在可逆对称张量空间中定义(没有偏差要求)。J_3在可逆对称张量空间上的梯度由式(7)给出——定域不是一个向量空间，而是对称张量空间的一个开集，这就足够了。如果你现在问J_3在可逆偏对称张量空间上的梯度应该是什么，然后再用7中的公式减去它沿I/(√3)的分量就得到了上面的eqn(**)通过使用(8)和(9)这对对称偏张量是有效的。

所以d J_3/ds在对称可逆偏张量空间上是一样的不管你用什么公式。当然，修正后的方法2更一般因为它给出了整个对称偏张量空间的公式。

所以我总结一下当你写dJ_3/ds时你要找的是函数det(s)在(线性)流形/二阶张量的向量空间的子空间上的梯度由tr(s) = 0定义。这需要一点小心，但这一切都是一致的

我希望这对你有帮助。

»
贾汉沙希先生的照片

提交的m . Jahanshahi星期二，2012-02-28 03:45。

亲爱的Acharya教授:

表达式

dJ_3/ds = s²- (1/3)(s²:I)I

实际上意味着我们在计算与约束流形相切的张量。这是前面文章中推导的关键区别。但问题是我们如何计算这个流形的法向量(或者这个流形的方程是什么)以及为什么J_3的导数应该与约束流形相切(在某种意义上是约束流形的协变导数)?

问候

Mohsen

»
Amit Acharya的照片

提交的Amit Acharya星期二，2012-02-28 10:15。

你关于导数与约束流形相切的评论是正确的——参见我在这篇文章早些时候(从很久以前)发表的题为“微分”的评论。

流形的方程是tr(s) = 0(它实际上是对称二阶张量空间的线性子空间)对于可逆部分，我们需要做一些繁琐的工作但事情就像你不需要担心可逆部分一样。

计算法线的方法就像在高级微积分中学习的那样——计算定义水平集的函数的梯度。假设二阶张量空间上的Froebenius范数(即迹内积度规)在形成单位法线时涉及到此计算。

看看我上面关于“微分”的评论，并告诉我这是否澄清了你的问题，为什么流形上J_3的“导数”应该与约束流形相切。

»
贾汉沙希先生的照片

提交的m . Jahanshahi星期三，2012-02-29 01:52。

亲爱的Acharya教授:

如果我是对的，这意味着我们想让导数保持在约束流形上，如果不是这样，约束就没有意义了(偏对称可逆张量的导数和对称可逆张量的导数之间没有区别)。但是作为这个约束的结果，所有偏对称可逆张量的导数都应该是无迹的(例如我们讨论的dJ_3/ds)。应该是这样吗?

Mohsen

»
Amit Acharya的照片

提交的Amit Acharya2012-02-29(星期三)10:00。

在你上面所说的一切，我怀疑你指的是(偏对称)张量的实值函数的导数，而不是张量本身的导数。关于你所问问题的答案，请参阅我在2月26日题为“Re:J3衍生品”的帖子中的评论，第2项)。

在有限维向量空间中，具有内积的可微实值函数的梯度必须是该空间的一个元素，其原因并不是因为人们“想”这样做——这是一个定理。在这一点上，认识到实值的导数也是一个好主意(如果你不熟悉这些概念，可以查阅一本关于高级微积分的好书，例如弗莱明-几个变量的函数)。fn。在向量空间上是一个到实数的线性变换(通常称为线性泛函)。因此，它不是空间本身的成员。然而，线性泛函有一个非常重要的表示定理(在有限维情况下很容易证明)，它表明向量空间上的每个线性泛函L都可以由空间本身中的一个唯一元素L来表示，使得

L(h) = L h对于向量空间中的所有h。如果L是fn实值的导数。我们认为，l是函数的梯度。

在我们的讨论中，det(S)和(1/3)tr(S ^3)是偏对称张量集合上的等实值函数。因此，只有要求它们的导数，或上述意义上的梯度，在这个空间中相等才有意义。但是梯度是偏对称张量空间的成员。

从上面的定义你现在可以看到为什么，如果一个函数在整个空间上有梯度，减去梯度在子空间法线上的投影就会得到这个函数在子空间上的限制的唯一梯度的正确答案。

»
贾汉沙希先生的照片

提交的m . Jahanshahi周六，2012-03-03 13:45

亲爱的Acharya教授:

在我之前的文章中，我指的是(偏对称)张量的实值函数的导数(比如我们讨论的那个张量的不变量)，当然不是张量值函数。顺便说一下，你关于(偏对称)张量的实值函数的梯度和导数的评论很有帮助。

谢谢

Mohsen

»
阿提拉·科萨的照片

提交的阿提拉Kossa星期二，2012-02-28 04:28。

我的问题是关于实值对称二阶可逆张量的年代．

的导数只存在一个解J3关于年代．

在一般情况下，J2不是零。然而，Method1和Method2是相同的，只有当J2= 0。

但是，我对这个案子很感兴趣J2不是= 0,J3不是= 0。

因此，我仍然感到惊讶的是，为什么在教科书中存在两个替代品。

推导过程中产生两个解的“棘手”步骤在哪里?

阿提拉

»
Amit Acharya的照片

提交的Amit Acharya星期二，2012-02-28 10:05。

我给出了J_3梯度的唯一解作为对称偏可逆张量的函数，以及对称偏张量的函数。J2不一定等于0，这个答案才有效。

我还没有检查课本上关于J2在对称偏可逆张量空间上的梯度的确切表述。然而，你的推导出错的地方是在解释(11)中的第一个等式时，第一个平等，在整个对称张量空间上是有效的。这不是真的。式(11)中的第二个等式，第二个平等，在整个空间都是正确的。如果你把注意力限制在J_3确实等于1/3tr(s^3)的子集上，即偏张量，在这个集合上，两个导数确实匹配，正如我所展示的。

也许在一个简单的设置中更容易看到发生了什么-取两个定义在x-y平面上的实值函数。让这两个函数在x-y平面上的一条直线上一致，所以想象两个任意相交于一条直线上的曲面。仅仅因为这两个函数的值在直线上匹配就认为它们的梯度在任何地方都相等是合理的吗?即使在直线上，期望函数的“导数”在它们有共同值的直线以外的方向上相等是合理的吗?当然，如果你把注意力集中在沿直线的函数上，那么期望这两个函数在直线上的限制的导数应该完全相等是非常合理的，事实上这就是所发生的。

有道理吗?

»
阿提拉·科萨的照片

提交的阿提拉Kossa周日，2012-02-26 02:48。

这是显而易见的。

我没有写Tr[s]。

Tr[s^2]和Tr[s^3]不为0。

阿提拉

»
订阅关于“张量不变量的导数”的评论

最近的评论

更多的评论

辛迪加

认购辛迪加